Day 17
Math 216: Statistical Thinking
Bastola
Recap: Steel Sheets Thickness
- Context: We revisit the scenario from Section 6.1 where a steel manufacturer’s rolling machine produces sheets of varying thickness, distributed uniformly between 150 and 200 millimeters.
- Experiment Setup: Random sampling of 11 steel sheets to measure thickness, repeated across 1000 samples.
Example 6.1
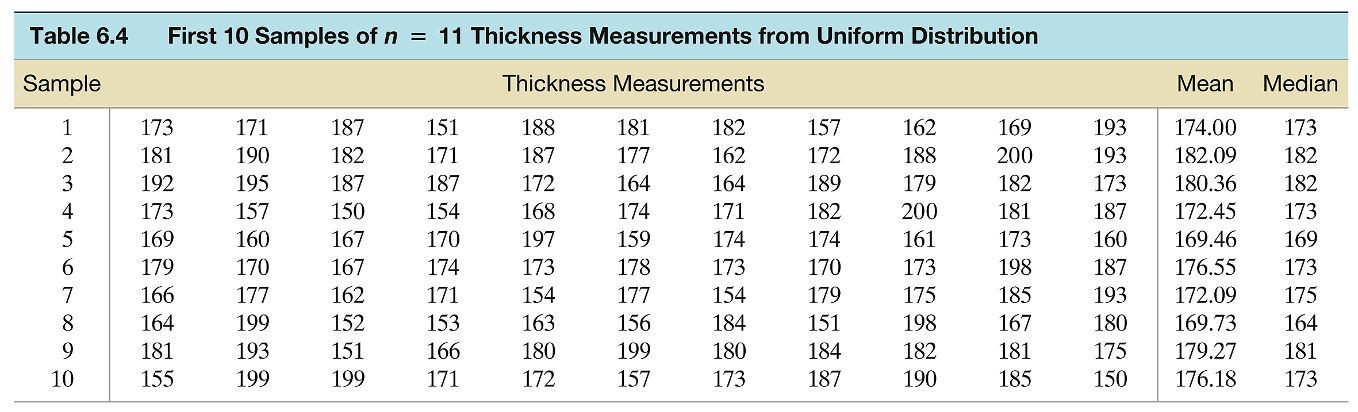
Sampling distribution for \(\bar{x}\)

Uniform Distribution Parameters
- Distribution Type: Uniform, with each value between 150 and 200 mm equally likely.
- Calculated Mean: \(\mu = \frac{150 + 200}{2} = 175\) mm.
- Calculated Standard Deviation: \(\sigma = \sqrt{\frac{(200 - 150)^2}{12}} \approx 14.43\) mm.
Sample Mean and Estimation
- Sample Mean: \(\bar{x} = \frac{\sum x}{11}\)
- Role of Sample Mean: Serves as a better statistic to approximate the population mean, especially useful when population parameters are unknown.
- Unbiased Estimator: \(\bar{X} = \frac{1}{n} \sum X_i\) is unbiased, meaning \(E(\bar{x}) = \mu\).
Properties of the Sampling Distribution
- Mean of Sampling Distribution: Equals the population mean, i.e., \(E(\bar{x}) = \mu\).
- Standard Error of the Mean (SE): \(\sigma_{\bar{x}} = \frac{\sigma}{\sqrt{n}}\) for sample size (n).
- Implication: The standard error quantifies the spread of the sampling distribution around the population mean.
Central Limit Theorem (CLT)
- Theorem Statement: For any population with mean \(\mu\) and standard deviation \(\sigma\), the sampling distribution of the sample mean \(\bar{x}\) will be approximately normal if the sample size \(n\) is sufficiently large (typically \(n \geq 30\)).
- Application: This theorem applies regardless of the original population’s distribution, making it a powerful tool in statistical inference.
Impact of Sample Size
- Visualization: Tells us how increasing sample size narrows the spread of the sampling distribution, aligning closer to a normal distribution.
- Practical Implication: Larger sample sizes lead to more precise estimations of the population mean, emphasizing the importance of sample size in experimental design.

Normal Approx. for Poisson
- Poisson Properties: For \(X \sim \text{Poisson}(\lambda)\):
- Mean: \(\mu = \lambda\)
- Variance: \(\sigma^2 = \lambda\)
- Shape: Right-skewed for small \(\lambda\), but becomes approximately normal as \(\lambda\) grows (\(\lambda > 10\) is often sufficient).
- Mean: \(\mu = \lambda\)
- Central Limit Theorem (CLT):
For large sample sizes \(n\), the sampling distribution of \(\bar{X}\) is approximately normal:
\[ \bar{X} \approx N\left(\mu_{\bar{x}} = \lambda,\ \sigma_{\bar{x}} = \sqrt{\frac{\lambda}{n}}\right) \]
Even if the population is Poisson, the sample mean becomes normal when \(n\) is large.