Day 19

Math 216: Statistical Thinking

Bastola

Estimation in Statistics

Objective: Use sample data to estimate population parameters.
Target Parameter: Unknown population parameter of interest.

Target Parameters

Types of Estimators

Point Estimator: A single value estimate of a population parameter.
- Example: \(\bar{x} = \frac{1}{n} \sum_{i=1}^n x_i\) estimates the population mean \(\mu\).
Interval Estimator (Confidence Interval): A range of values to estimate the parameter with a specified level of “confidence”.

Importance of Confidence Intervals

Confidence Interval: Not just a point estimate, but an interval that likely contains the target parameter.
Reliability: Provides a measure of the reliability of the estimate.

Calculating a Confidence Interval

Scenario: Estimating average hospital stay length.
Sample Data: Sample mean \(\bar{x}\) from 100 patient records.
Central Limit Theorem: Assures that \(\bar{x}\) is approximately normally distributed for large samples.

Confidence Interval Formula

95% Confidence Interval for \(\mu\): \[ 95\% \text{ C.I.} = \left(\bar{x} - 1.96 \frac{\sigma}{\sqrt{n}}, \quad \bar{x} + 1.96 \frac{\sigma}{\sqrt{n}}\right) \]
Note: \(\sigma\) is the standard deviation of the population, and \(n\) is the sample size.

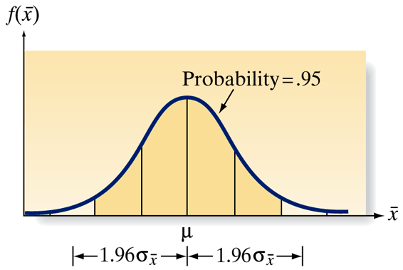
Understanding Confidence Intervals

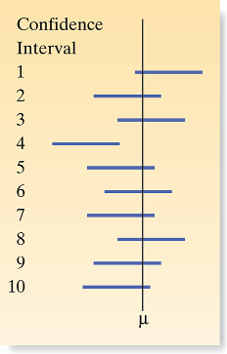
Question: Is the true mean \(\mu\) between 3.81 and 5.25?
Confidence Understanding:
- No certainty that \(\mu\) lies within this specific interval from a single sample.
- If repeated samples are taken, about 95% of such intervals would contain \(\mu\).
Correct Interpretation:
- We don’t say \(\mu\) is definitely in this interval based on one sample; the 95% level reflects how often these intervals capture \(\mu\) across many samples.
Terminology:
- Confidence Coefficient (.95): Proportion of intervals that will contain \(\mu\) over repeated sampling.
- Confidence Level (95%): Indicates method reliability over many trials.

Understanding CIs

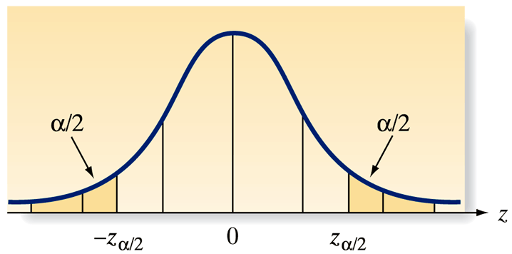
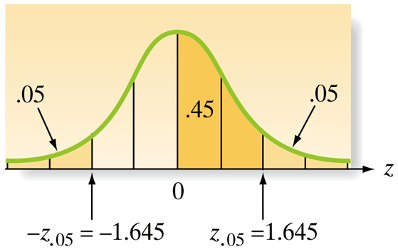
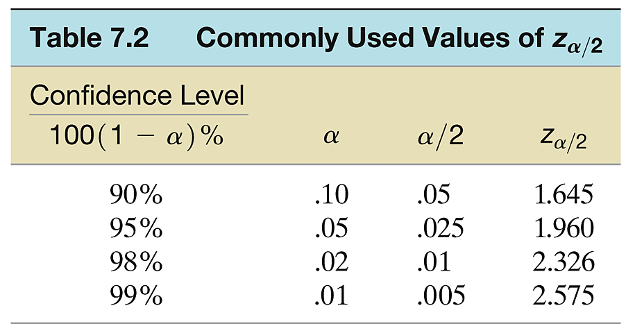
Commonly used values of \(z_{\alpha}\)

The value \(z_\alpha\) is defined as the value of the standard normal random variable \(z\) such that the area \(\alpha\) will lie to its right. In other words, \(P\left(z>z_\alpha\right)=\alpha\).