Day 20

Math 216: Statistical Thinking

Bastola

Introduction to Small Samples and the t-Statistic

• Small Samples: In research, we sometimes only have access to a small number of observations, which limits the effectiveness of the Central Limit Theorem.
• Need for a Different Approach: Traditional z-statistics assume a large sample size to normalize sample means, which is not feasible with small samples. This session introduces the student’s t-statistic, a better-suited approach for such scenarios.

Challenges with Small Samples

• Normality Assumption: For samples smaller than 30, the distribution of the population must be approximately normal for the sample mean \(\bar{x}\) to be considered normally distributed. For example, if you’re studying the heights of a rare species of plant, and can only find a few samples, the underlying distribution of these heights must be normal for standard approaches to work.
• Standard Deviation Issues: When using the sample standard deviation \(s\) in place of the population standard deviation \(\sigma\), the estimate becomes less reliable with smaller samples. Consider a scenario where you measure the amount of a chemical in water samples from different locations. With only a few samples, the variability in your measurements could significantly affect the reliability of your estimates, leading to potentially misleading conclusions.

Introducing the Student’s t-Statistic

Given the issues identified with small samples, the Student’s t-statistic offers a refined method for estimating population parameters: \[ T = \frac{\bar{x} - \mu}{s / \sqrt{n}} \] This formula adjusts for the additional uncertainty inherent in small samples.

Comparison with the z-Statistic

The t-statistic is analogous to the z-statistic used for larger samples, where the population standard deviation \(\sigma\) is known or the sample is large enough (\(n \geq 30\)) for reliable approximation: \[ Z = \frac{\bar{x} - \mu}{\sigma / \sqrt{n}} \]

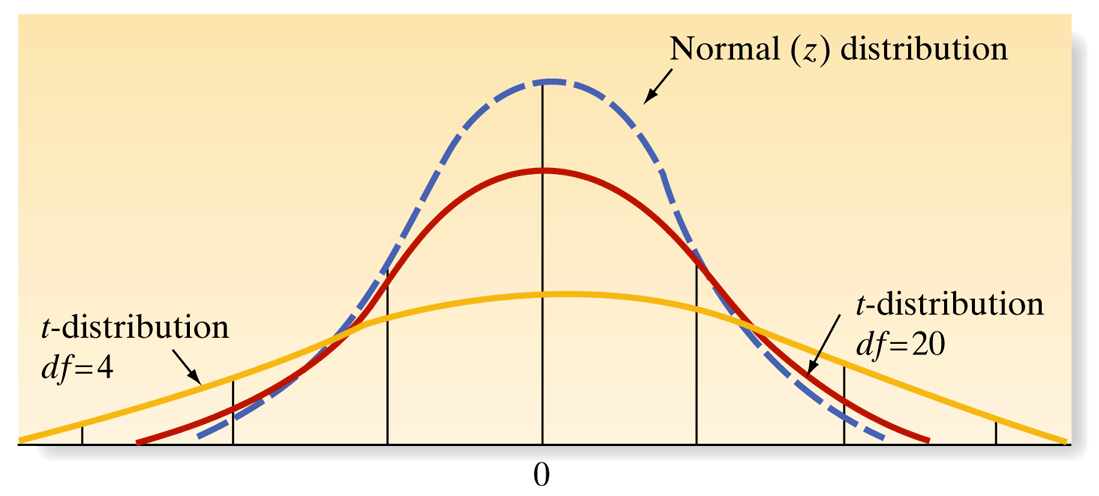
Why Use the t-Distribution?

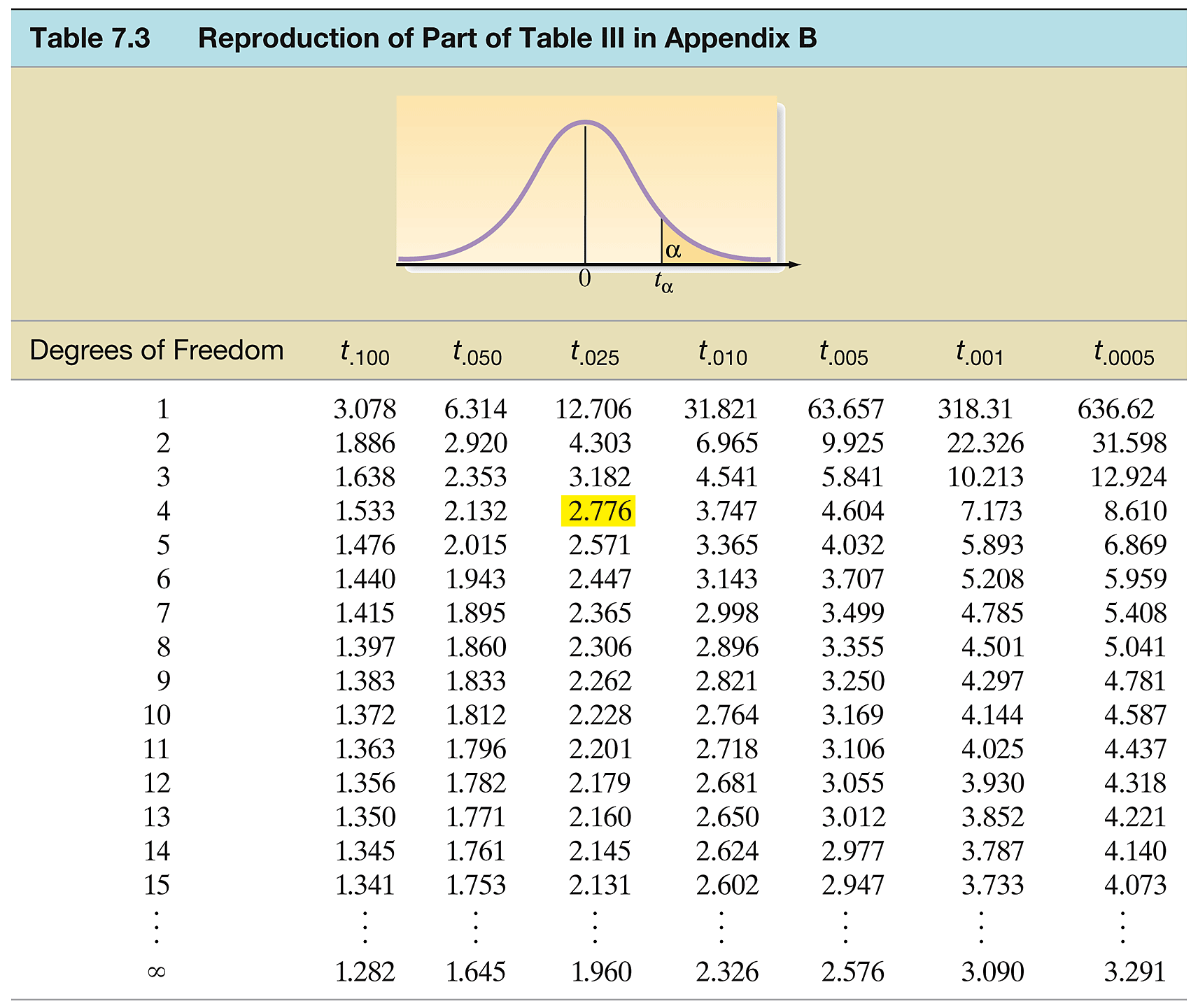
• Degrees of Freedom: The shape of the t-distribution and its variability depend on the degrees of freedom (df = \(n-1\)), which adjusts as the sample size changes. This flexibility makes it particularly useful for small sample sizes.

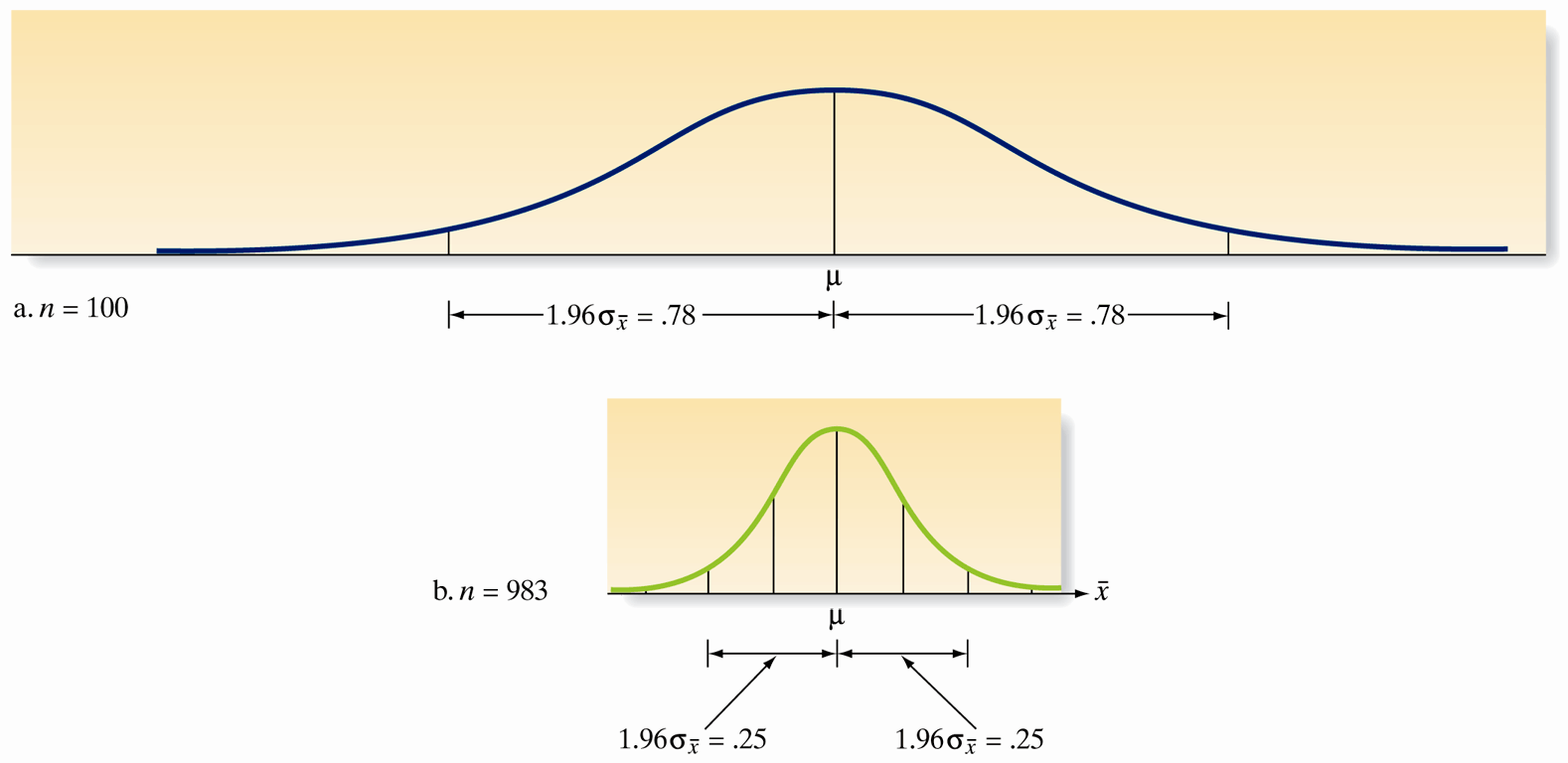
Overview of Determining Sample Size

• Importance of sample size in designing experiments.
• Impacts the reliability of inferences about a population mean.