Day 21

Math 216: Statistical Thinking

Bastola

Sampling Distribution of \(\hat{\boldsymbol{p}}\)

1. Mean of Sampling Distribution: \(\hat{p}\) is an unbiased estimator of \(p\), i.e., the mean of the sampling distribution of \(\hat{p}\) is \(p\).
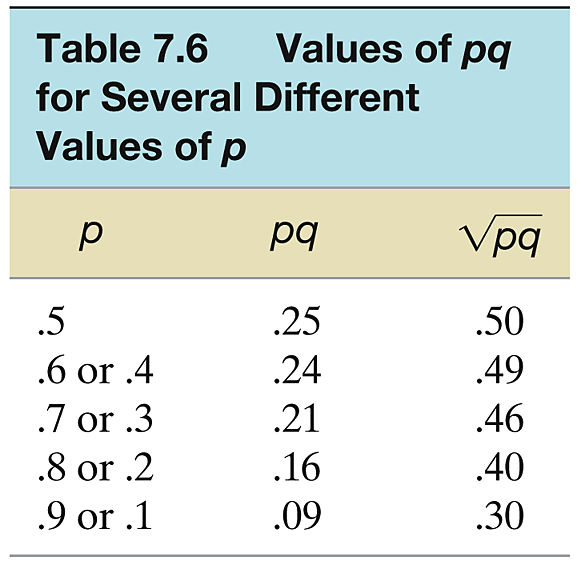
2. Standard Deviation: \(\sigma_p=\sqrt{\frac{p q}{n}}\), where \(q=1-p\).
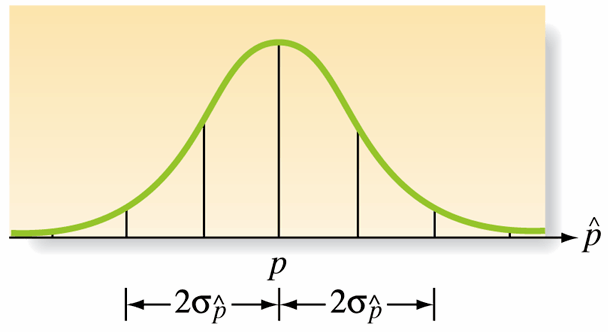
3. Approximation to Normality: For large samples, the distribution of \(\hat{p}\) is approximately normal, valid if \(n \hat{p} \geq 15\) and \(n \hat{q} \geq 15\).

Sampling Distribution of \(\hat{\boldsymbol{p}}\)

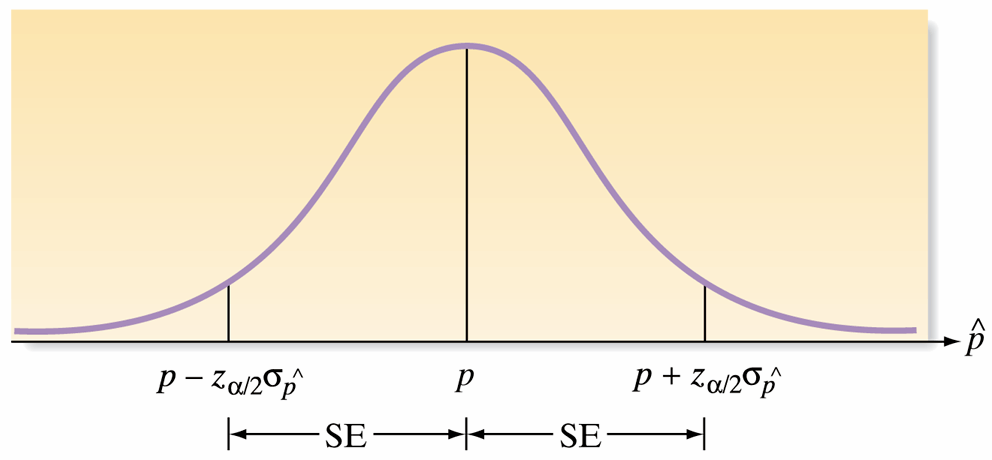
Large-Sample Confidence Interval for \(p\)

• Formula: \(\hat{p} \pm z_{\alpha / 2} \sqrt{\frac{\hat{p} \hat{q}}{n}}\)
• \(\hat{p}=\frac{x}{n}\), \(\hat{q}=1-\hat{p}\)
• Assumes \(n\) is large enough for normal approximation.

Conditions for Valid Large-Sample C.I. for \(\boldsymbol{p}\)

1. Random sample from the target population.
2. Large sample size, quantified by \(n \hat{p} \geq 15\) and \(n \hat{q} \geq 15\).

Values of \(pq\) for different \(p\)