Day 22

Math 216: Statistical Thinking

Bastola

Introduction to Hypothesis Testing

• Hypothesis testing is a statistical method used to decide whether to support or refute a specific claim about a population parameter based on sample data.
• Analogous to a judicial process: The null hypothesis (\(H_0\)) represents the “status quo” (e.g., “innocent until proven guilty”).

Elements of a Test of Hypothesis

• City regulations require residential sewer pipes to have an average breaking strength greater than 2,400 pounds per foot.
• Manufacturers must demonstrate that their products meet this standard.

Hypotheses

• Null Hypothesis (\(H_0\)): In theory, \(\mu \leq 2400\). If we reject \(\mu = 2400\), \(\mu < 2400\) is also rejected.
• Alternative Hypothesis (\(H_a\)): \(\mu > 2400\) (Pipes meet or exceed the standard).

Testing the Hypothesis

Computation of Test Statistic

• By the Central Limit Theorem, for large samples (\(n \geq 30\)), \(\bar{x}\) approximates a normal distribution.
• Test statistic \(z\): \[ z = \frac{\bar{x} - \mu_0}{\sigma/\sqrt{n}} \] where \(\sigma\) is the population standard deviation and \(\mu_0 = 2400\).

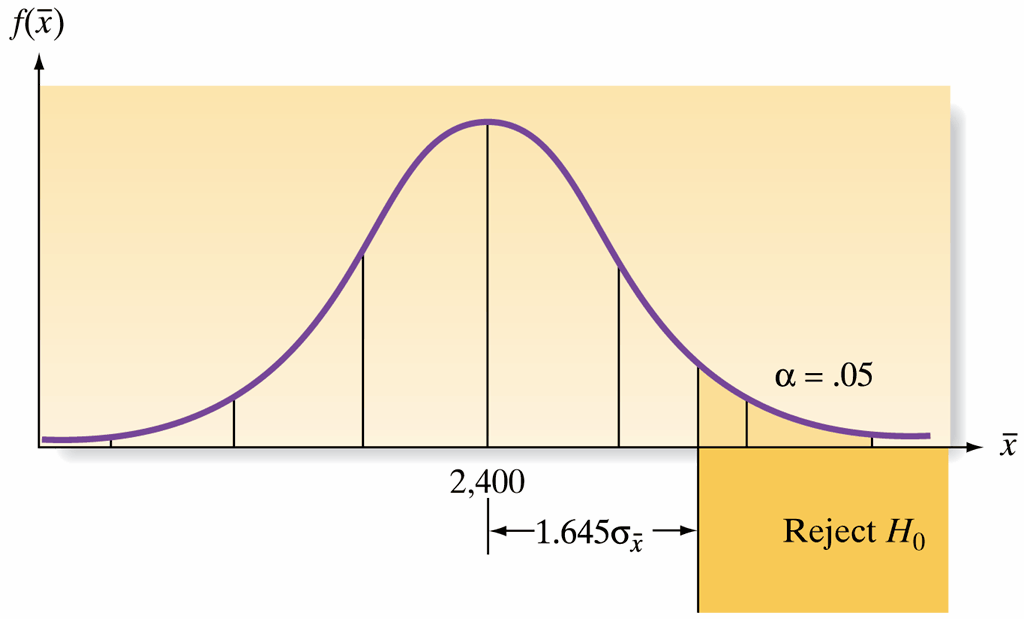
Decision Making

• If the observed \(\bar{x}\) exceeds 1.645 standard deviations above 2,400, we consider rejecting \(H_0\).
• Rejection implies that a rare event (occurring with probability \(\leq 0.05\) under \(H_0\)) is unlikely without true cause (i.e., \(H_a\) is likely true).

Evidence from Sample Data

• Sample Characteristics:
  • Number of samples (\(n\)): 50
  • Mean strength (\(\bar{x}\)): 2,460 pounds per linear foot
  • Standard deviation (\(s\)): 200 pounds per linear foot
• Test Statistic Calculation:
  • The test statistic (\(z\)) is calculated as follows: \[ z = \frac{\bar{x} - 2400}{s/\sqrt{n}} \approx \frac{2460 - 2400}{200 / \sqrt{50}} = \frac{60}{28.28} \approx 2.12 \]

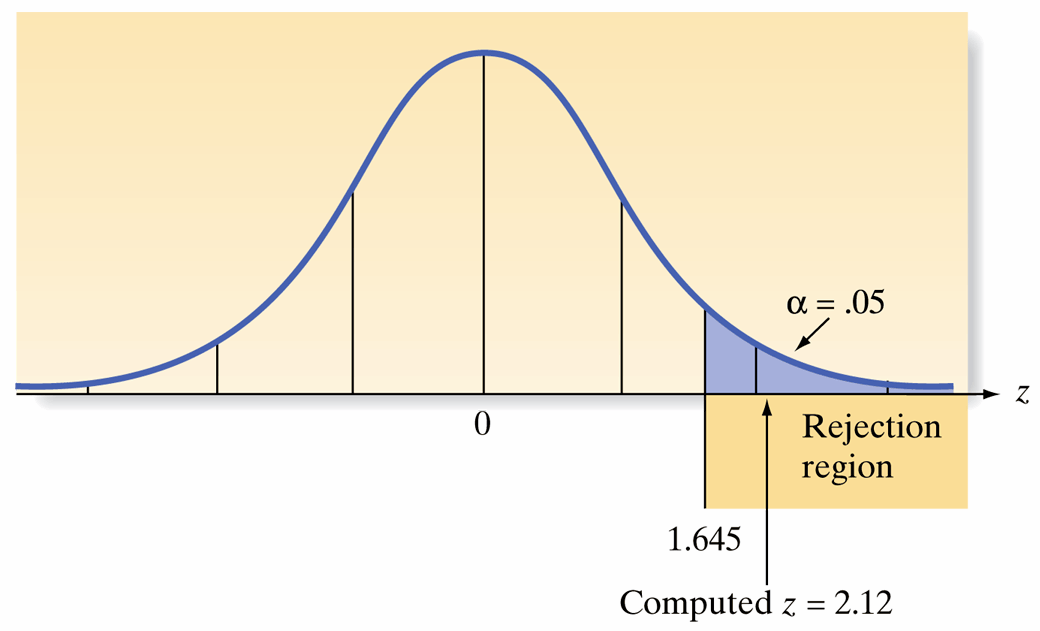
Types of Errors

Type I Error

• Analogy: Convicting an innocent person.
• Occurs if we reject \(H_0\) when it is, in fact, true.
• Probability of Type I error is denoted by \(\alpha\) (commonly set at 0.05).

Types of Errors

Type II Error

• Analogy: Acquitting a guilty person.
• Occurs if we fail to reject \(H_0\) when, in fact, \(H_a\) is true.
• Probability of Type II error is denoted by \(\beta\).
• Unlike \(\alpha\), \(\beta\) is not usually pre-specified but affected by the sample size, effect size, and the set \(\alpha\).

Types of Errors

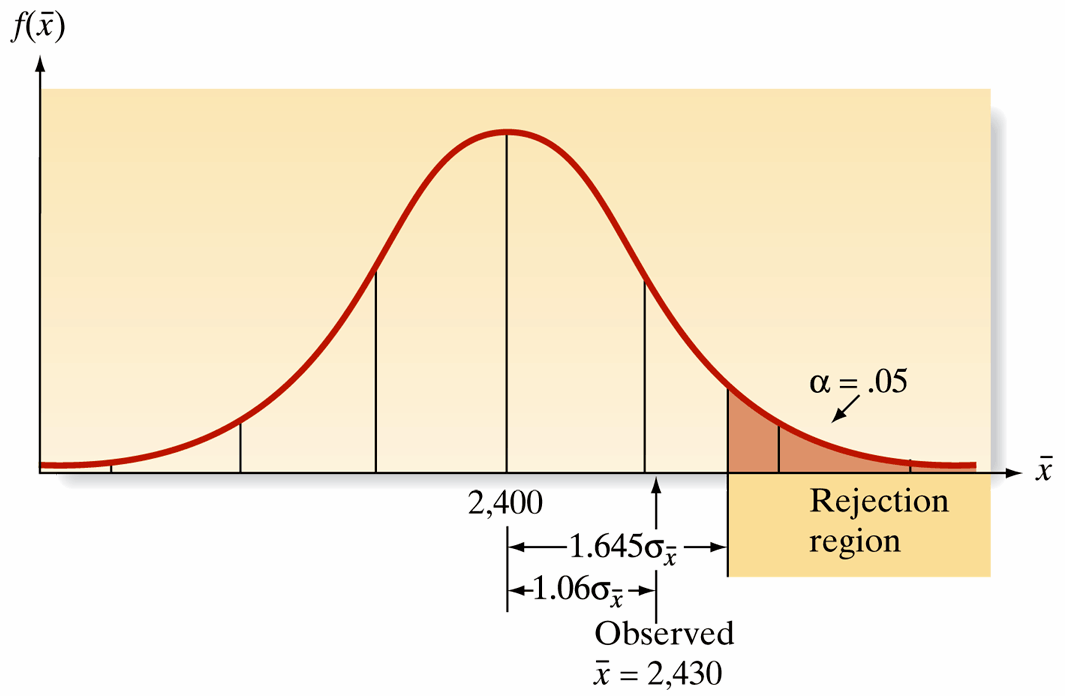
Rejection Region

• The set of values of the test statistic that lead us to reject \(H_0\).
• For this test, it’s values greater than the z-value corresponding to a 0.05 probability in the upper tail of the normal distribution.

Summary

• Hypothesis Testing as a Judicial Process:
  • \(H_0\): The defendant (population parameter) is presumed innocent (equals 2400) until proven otherwise.
  • \(H_a\): Claims the defendant is not innocent (greater than 2400).
  • We examine the “evidence” (sample data) to decide whether it sufficiently supports \(H_a\) over \(H_0\).