Day 25

Math 216: Statistical Thinking

Bastola

Introduction to Small Sample Confidence Intervals

• Background: Confidence intervals and hypothesis testing for large samples (\(n \geq 30\)) rely on the \(z\)-statistic.
• Challenge: What happens with a small sample size (\(n < 30\)) where the Central Limit Theorem does not apply?

Adjusting for Small Samples

• Population Distribution: If the sample comes from an approximately normal distribution, we can use the \(t\)-statistic.
• Standard Deviation: When the population standard deviation \(\sigma\) is unknown and \(n < 30\), using the sample standard deviation \(s\) to approximate \(\sigma\) is unreliable.
• Solution: \[ t=\frac{\bar{x}-\mu}{s / \sqrt{n}} \]
  • Follows a \(t\)-distribution with degrees of freedom, \(df = n-1\).

Confidence Interval Using Student’s t-Statistic

• When \(\sigma\) is unknown: Use the \(t\)-statistic for confidence intervals.
  • For a \(95\%\) confidence interval: \[ \bar{x} \pm t_{\alpha/2} \left(\frac{s}{\sqrt{n}}\right) \] where \(t_{\alpha/2}\) is determined from the \(t\)-distribution table for \(df = n-1\).

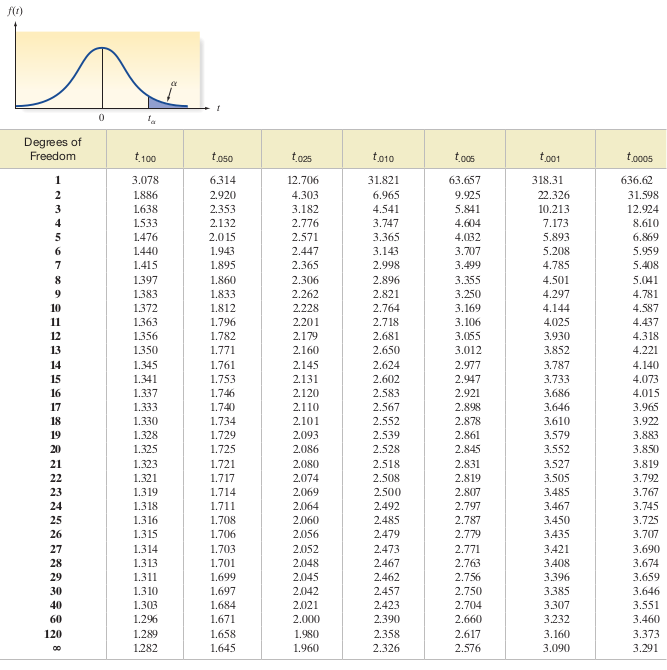
Calculation of P-Value

• When \(n<30\) and \(\sigma\) is unknown:
  • Use Case: If the population is approximately normally distributed.
  • Student’s t-Statistic: \[ t = \frac{\bar{x} - \mu_{0}}{s / \sqrt{n}} \]
    • Follows a \(t\)-distribution with \(df = n - 1\).