Day 31
Math 216: Statistical Thinking
Bastola
Review: Mean vs. Proportion
- Previously studied: Confidence intervals (C.I.) and hypothesis tests for population means.
- Non-parametric tests were focused on population medians.
Transition to Proportions
- Now focusing on population proportion (e.g., “What percentage of voters favor candidate A?”)
- Applies similar principles as the Central Limit Theorem for means, using properties of the sampling distribution of \(\hat{p}\).
Properties of \(\hat{p}\)
- Mean: The expected value (mean) of \(\hat{p}\) is equal to the true population proportion \(p\). \[ E(\hat{p}) = p \]
- Standard Deviation: For large samples, approximated by \[ \sigma_{\hat{p}} \approx \sqrt{\frac{\hat{p}(1-\hat{p})}{n}} \]
- Distribution: Becomes approximately normal with large sample sizes.
Large-Sample Hypothesis Testing
- Test Statistic: Normal (z) statistic for \(H_0: p = p_0\): \[ z_c = \frac{(\hat{p} - p_0)}{\sqrt{\frac{p_0(1-p_0)}{n}}} \]
- Decision Rule: Reject \(H_0\) if p-value \(< \alpha\), or if \(z_c\) falls into the rejection region.
Hypothesis Test Types
- One-Tailed Test:
- \(H_a: p < p_0\) or \(H_a: p > p_0\)
- Rejection region: \(z_c < -z_{\alpha}\) or \(z_c > z_{\alpha}\)
- Two-Tailed Test:
- \(H_a: p \neq p_0\)
- Rejection region: \(z_c < -z_{\alpha/2}\) or \(z_c > z_{\alpha/2}\)

Conditions for Testing
- Random sample from the population.
- Large enough sample size, typically \(n\hat{p} \geq 15\) and \(n\hat{q} \geq 15\).
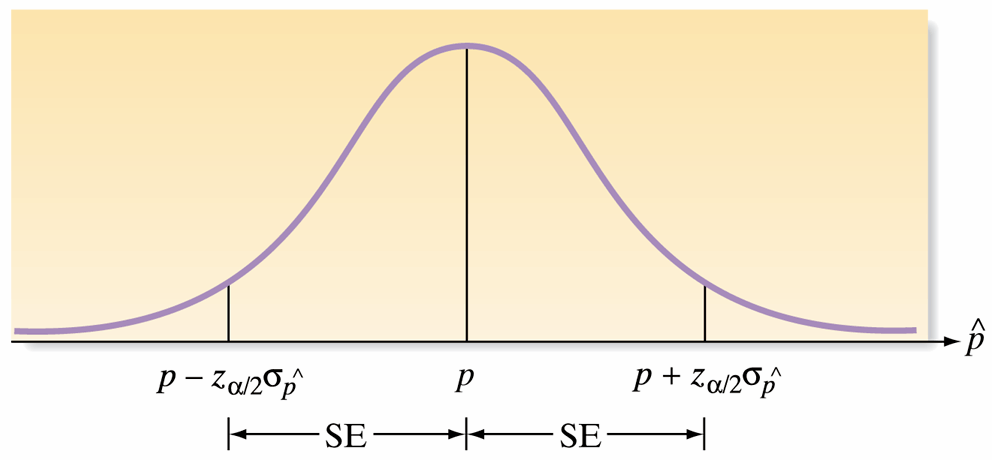
Confidence Interval for \(\hat{p}\)
- Large-sample confidence interval: \[ \hat{p} \pm z_{\alpha/2} \sqrt{\frac{\hat{p}(1-\hat{p})}{n}} \]
- Valid when \(n\) is large for normal approximation.
Sample Size Determination
- To specify sampling error (SE) and confidence level: \[ n = \frac{(z_{\alpha/2})^2 \hat{p}(1-\hat{p})}{SE^2} \]
- Conservative estimate uses \(p \approx 0.5\) when \(\hat{p}\) is unknown.
