Day 32
Math 216: Statistical Thinking
Understanding Type II Errors in Hypothesis Testing
Type I Error (\(\alpha\)): Rejecting the null hypothesis \(H_0\) when it is true. The probability of making a Type I error is controlled by the rejection region.
Type II Error (\(\beta\)): Accepting the null hypothesis \(H_0\) when it is false. Unlike \(\alpha\), \(\beta\) is not as easily controllable and varies with the true value of the parameter being tested against \(H_0\).
Error Types Table
| Decision / Null Hypothesis | \(H_0\) True | \(H_0\) False |
|---|---|---|
| Fail to Reject \(H_0\) | Correct Inference (True Negative) Probability = 1 - \(\alpha\) | Type II Error (False Negative) Probability = \(\beta\) |
| Reject \(H_0\) | Type I Error (False Positive) Probability = \(\alpha\) | Correct Inference (True Positive) Probability = 1 - \(\beta\) |
Example Hypothesis Setup
Null Hypothesis (\(H_0\)): \(\mu = 2400\)
Alternative Hypothesis (\(H_a\)): \(\mu > 2400\)
Test Statistic: \[ z = \frac{\bar{x} - 2400}{\sigma / \sqrt{n}} \]
Suppose \(\sigma_{\bar{x}} = 28.267\) and \(\bar{x} \sim N(\mu, 28.267)\).
Rejection region for \(\alpha = 0.05\) is \(z > 1.645\).
Visualization of the Rejection Region
The area in the rejection region under the null distribution (assuming \(H_0\) is true) is 0.05. This area represents \(\alpha\), the probability of rejecting \(H_0\) when it is in fact true.
- The figures illustrate \(\beta\) for \(\mu = 2425, 2450, 2475\).
- As \(\mu\) increases, \(\beta\) decreases, reflecting a lower risk of incorrectly accepting \(H_0\) as the true mean strength moves farther from \(2400\).
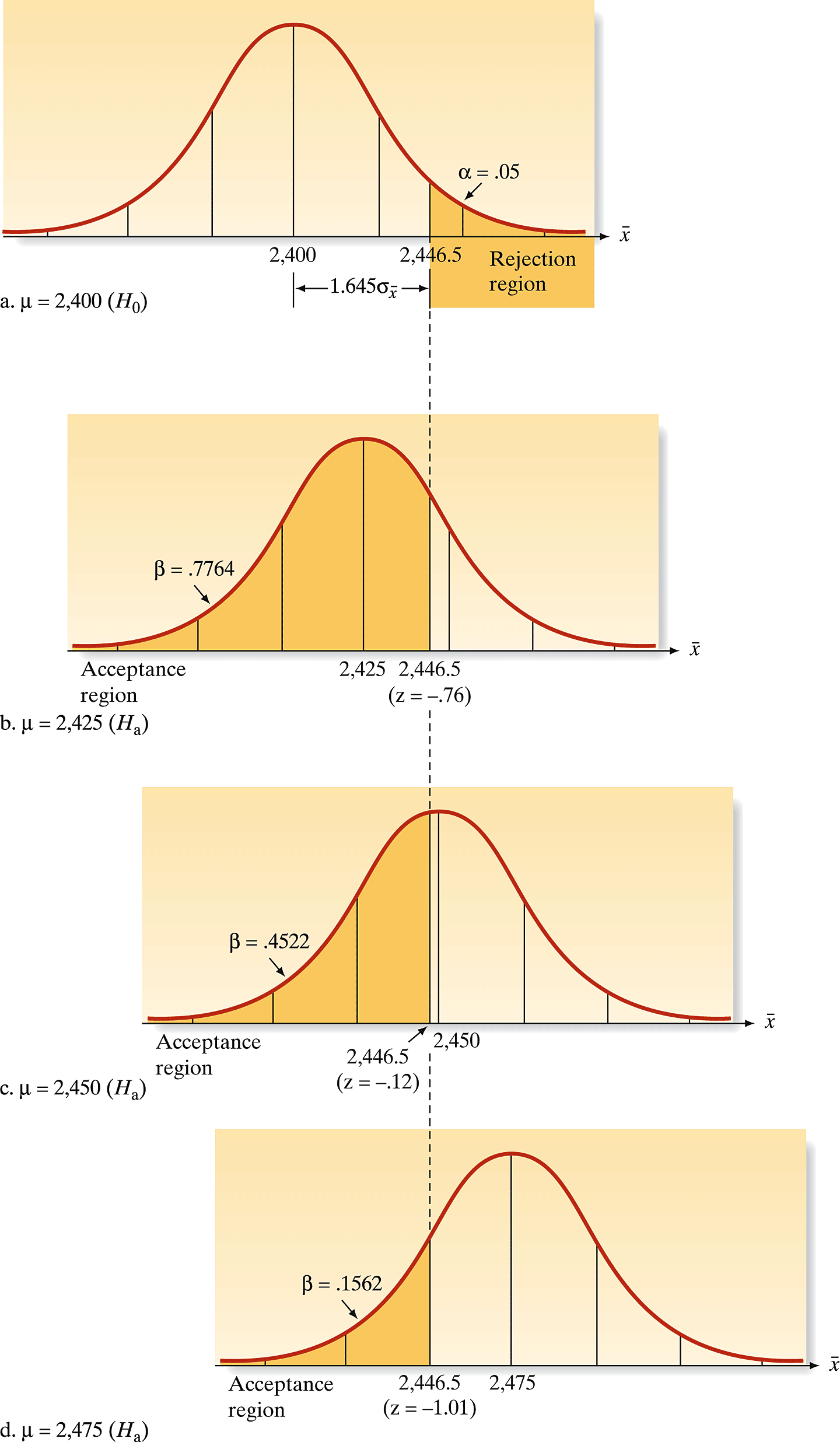
Calculating \(\beta\) for Different \(\mu\) Values
- The probability of a Type II error, \(\beta\), is defined under the assumption that the null hypothesis is false.
- \(\beta\) is calculated for each \(\mu > 2400\), reflecting the risk of accepting \(H_0\) when it is false.
- For \(\mu = 2425\), we find \(\beta\) as the area under the curve to the left of \(\bar{x} = 2446.5\):
\[ \beta = \operatorname{Prob}\left[\bar{x} < 2446.5 \mid \mu = 2425\right] = 0.7764 \]
The Power of the Test
- The power of a test is the probability that the test correctly rejects \(H_0\) for a specific \(\mu\) in \(H_a\).
- Calculated as \(1 - \beta\), the power increases as \(\beta\) decreases.
- Understanding \(\beta\) and the power of a test is crucial for assessing the effectiveness of hypothesis tests, especially when the true parameter differs significantly from the null hypothesis value.