Activity 16
MATH 216: Statistical Thinking
Activity 2: Conceptual understanding
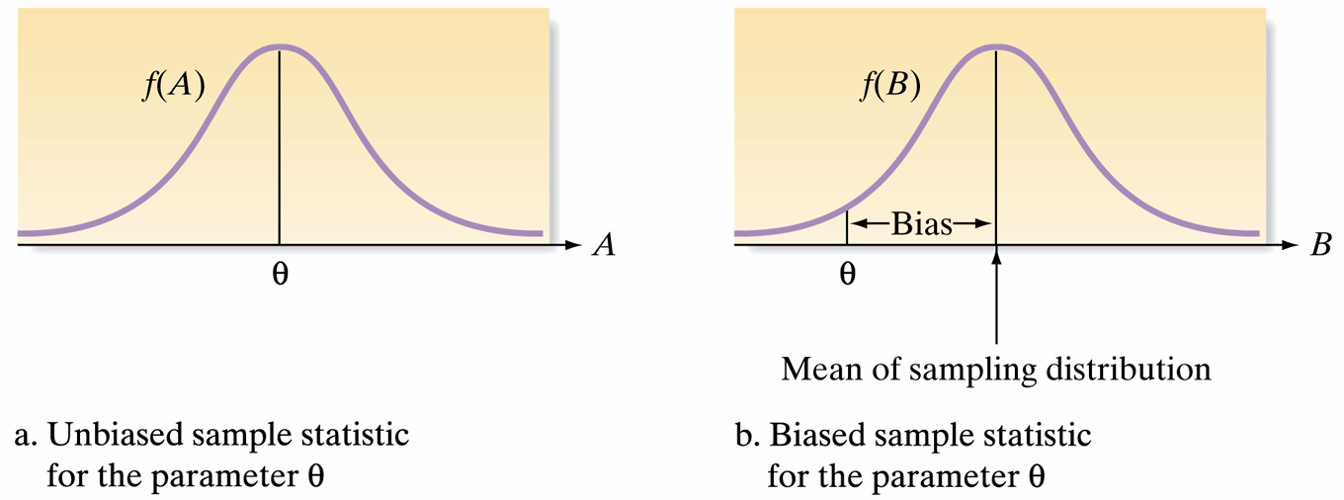
Suppose two statistics, \(A\) and \(B\), exist to estimate the same population parameter \(\theta\) (theta). (Note that \(\theta\) could be any parameter: \(\mu, \sigma^2\), etc.) Suppose the two statistics have sampling distributions as shown in the following figure. On the basis of these sampling distributions, which statistic is more attractive as an estimator of \(\theta\) ?
Activity 3: Quiz
- Question: What does the standard error measure in the context of sampling distributions?
A). The mean of the sampling distribution
B). The spread of the sampling distribution
C). The bias of the estimator
D). The population parameter
Activity 4: Group Activities with Real Data
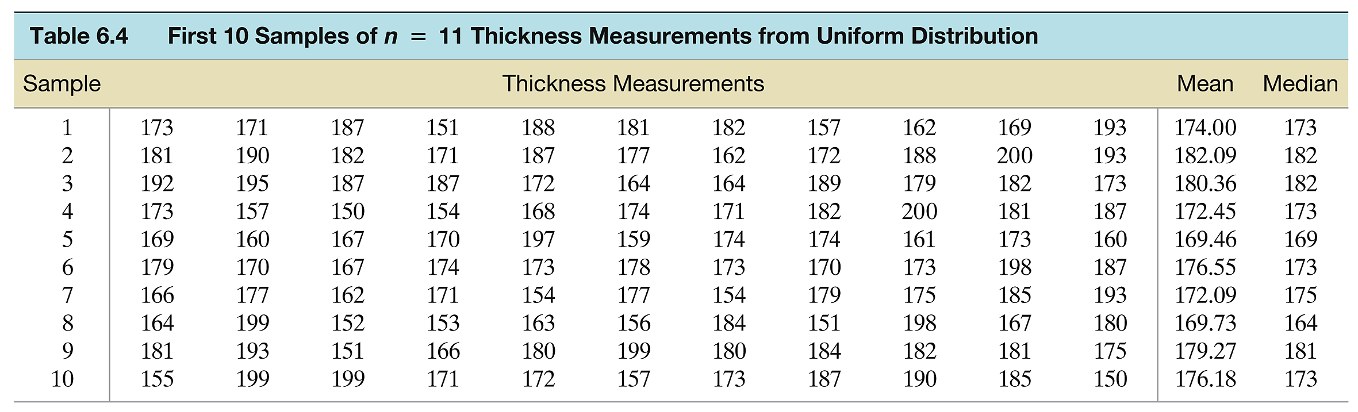
Prompt: The rolling machine of a steel manufacturer produces sheets of steel of varying thickness. The thickness of a steel sheet follows a uniform distribution with values between 150 and 200 millimeters. Suppose we perform the following experiment over and over again: Randomly sample 11 steel sheets from the production line and record the thickness x of each. Calculate the two sample statistics:
\[ \bar{x}=\text { Sample mean }=\sum x / 11 \]
\(M=\) Median = Sixth sample measurement when the 11 thicknesses 1 are arranged in ascending order Obtain approximations to the sampling distributions of \(\bar{x}\) and \(M\). Since we know that it is uniform distribution, the mean is 175 mm . But let’s assume that we don’t know that and just use the sampling to approximate the parameter.
- Analyze the steel thickness dataset.
- Compare the sampling distributions of \(\bar{x}\) and \(M\).
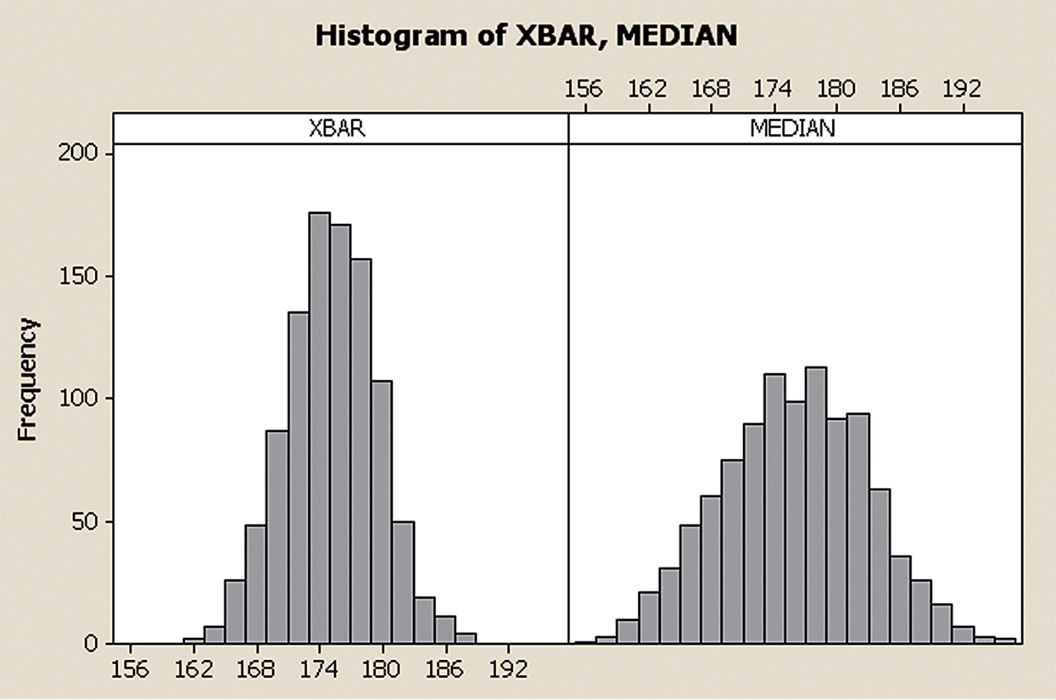
- Discuss which statistic (mean or median) is a better estimator of the population parameter and why.
Activity 5: Case Studies and Problem-Solving
Scenario: A factory produces steel sheets with thicknesses following a uniform distribution. The quality control team wants to estimate the average thickness using sample statistics.
Task: Apply the concepts of unbiasedness and standard error to determine whether the sample mean or median is a better estimator for the population mean.