Activity 21

MATH 216: Statistical Thinking

Activity 1: Quiz

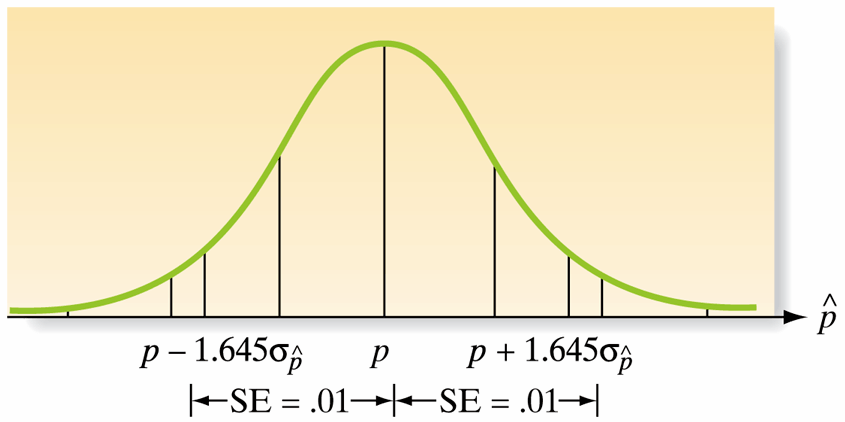
• Question: Given \(\hat{p} = 0.65\), \(n = 169\), and a 90% confidence level, calculate the confidence interval for \(p\). Use \(z_{\alpha/2} = 1.645\).

Activity 2: Case Studies and Problem-Solving

• Scenario: A political campaign wants to estimate the proportion of voters who support their candidate. They survey 500 voters and find that 300 support the candidate.
• Task: Apply the concepts learned to calculate a 95% confidence interval for the true proportion of supporters. Discuss the implications of the confidence interval width on the campaign’s strategy.

Activity 3: Sample Size Calulations

Building on the information and context from Activity 1, design a study where the goal is to calculate the required sample size to achieve a narrower margin of error for the population proportion \(p\). Assume a desired sampling error of 0.03 at a \(90 \%\) confidence level, maintaining the same population proportion estimate \((\hat{p}=0.65)\). How many individuals should be included in the new sample to meet these precision requirements? If you did not know \(p\) in advance, how would you estimate the sample size in advance for the same sampling error?

Activity 4: Sample Size Calulations

Using the setup of Activity 1, find the sample size needed for a SE of 0.01?