Activity 19
MATH 216: Statistical Thinking
Activity 1: Quiz
- Question: Given a sample mean \(\bar{x} = 5.2\), a population standard deviation \(\sigma = 2.5\), and a sample size \(n = 100\), calculate the 95% confidence interval for the population mean \(\mu\).
Activity 2: Data Exploration
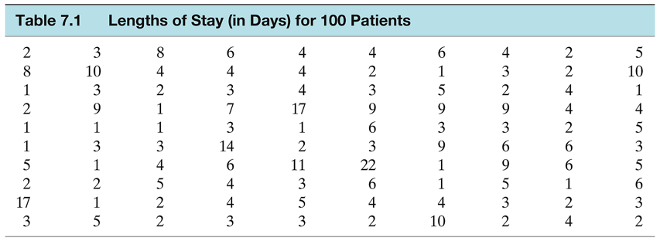
- Task: Use the following R-code output to calculate the sample mean and standard deviation, then infer the shape, mean, and spread of the population and sampling distribution.
Activity 3: Understanding Confidence Intervals
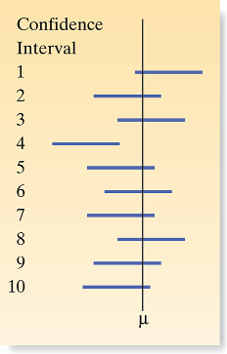
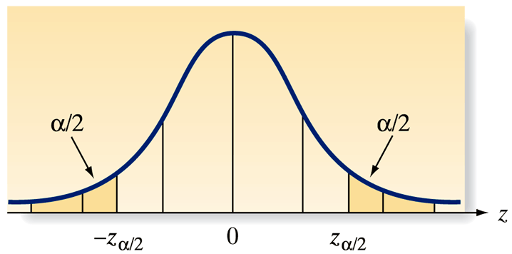
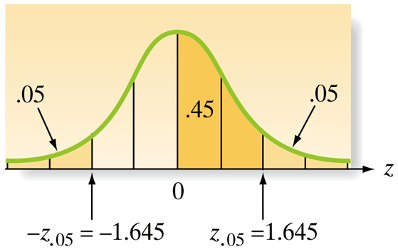
What is the correct interpretation of \(100(1-\alpha)\%\) confidence intervals for a mean of a population?
Activity 4: Group Activities with Real Data
- Task: Using the provided dataset in Activity 2, calculate a 95% confidence interval for the population mean \(\mu\). Interpret the results in the context of the problem.
Activity 5: Case Studies and Problem-Solving
- Case Study: A hospital wants to estimate the average length of stay for its patients. They have collected data from 30 patients and found a sample mean of 5 days with a standard deviation of 5 days. Calculate a 95% confidence interval for the average length of stay and interpret the results. Use the interval estimator \(\bar{x} \pm 1.96 \sigma_{\bar{x}}\) to calculate a confidence interval for the target parameter, \(\mu\).