Activity 18
MATH 216: Statistical Thinking
Activity 1: Quiz
Question: If \(p = 0.4\) and \(n = 50\), what is the standard deviation of \(\hat{p}\)?
- 0.069
- 0.049
- 0.089
- 0.029
Activity 2: Mean and Standard Deviation of \(\hat{p}\)
Task: The soft-drink cups at a certain fast-food restaurant have tickets attached to them. Customers peel off the tickets to see whether they win a prize. The proportion of tickets that are winners is \(p=0.25\). A total of \(n=70\) people purchase soft drinks between noon and 1:00 p.m. on a certain day. Let \(\hat{p}\) be the proportion that win a prize.
- Find the mean of \(\hat{p}\).
- Find the standard deviation of \(\hat{p}\).
Activity 3: Sampling Distribution of \(\hat{p}\)
Task: A study of city voters is taken to determine whether they are in favor of a certain candidate for mayor. We assume that \(60\%\) of all the city’s voters favor the candidate. Suppose we randomly sample 100 voters and ask each if they are in favor of the candidate. We want to study the sampling distribution of \(\hat{p}\), the sample proportion of voters in favor of the candidate.
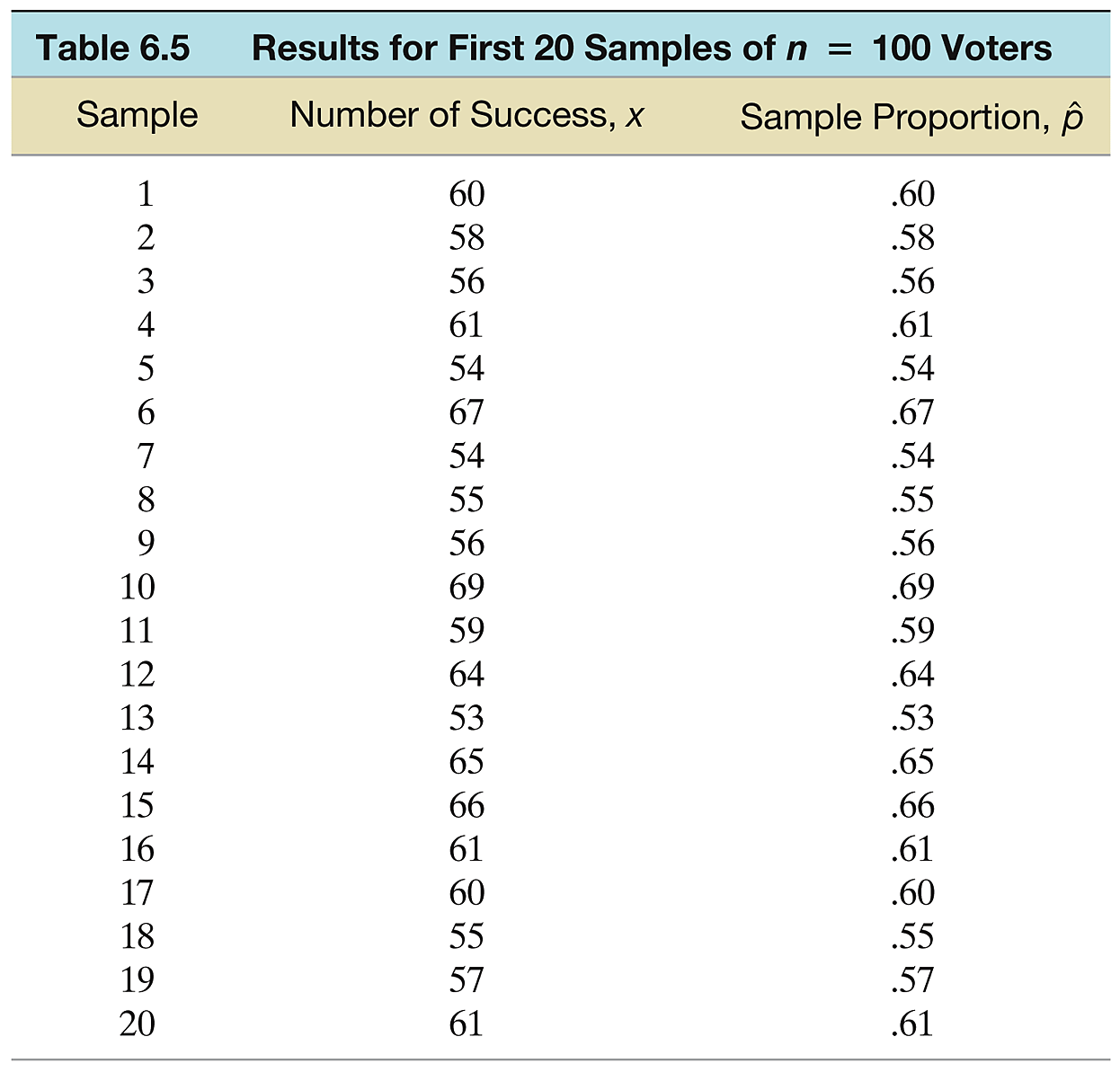
Questions:
- What is the mean of \(\hat{p}\)?
- What is the standard deviation of \(\hat{p}\)?
- What properties do you observe about the sampling distribution of \(\hat{p}\)?
Activity 4: Probability of Sample Proportion
Task: According to a Harris poll taken in September 2013, chocolate is the favorite ice cream flavor for \(27\%\) of Americans. If a sample of 100 Americans is taken, what is the probability that the sample proportion of those who prefer chocolate is greater than 0.30?
Questions:
- Calculate the mean and standard deviation of \(\hat{p}\).
- Use the normal approximation to find \(P(\hat{p} > 0.30)\).
Activity 5: Binomial Distribution:
A fair coin is flipped 200 times, with \(X\) denoting the number of heads (binomial distribution: \(n=200\), \(p=0.5\)). If 40 trials of 200 flips are conducted:
- Determine \(\mu_{\bar{x}}\) and \(\sigma_{\bar{x}}\) for the sample proportion of heads.
- What is the probability that the sample proportion differs from 0.5 by more than 0.04?